Selection Sort: Choosing the Right Element, One Pass at a Time

The Night I Finally Organized My Toolbox

It was 2:34 a.m. and my garage looked like a hardware store after an earthquake. Every drawer was chaos—screws mixed with nails, wrenches scattered like metallic confetti, and somewhere in that mess was the 10mm socket I desperately needed. I started the only way that made sense: scan everything, find the smallest item, put it in the first drawer. Then scan again, find the next smallest, put it in the second drawer. One selection per pass, methodical and predictable.

By 3:17 a.m., every tool had a home. The process was slow, but it was certain. Each item went exactly where it belonged, and once placed, it never moved again. No second-guessing. No adjustments. Just pure, mechanical precision.

That's Selection Sort.

Each pass looks at everything left, picks the best candidate, and places them where they belong. No bubbling. No shifting. No guessing. Just scanning and selecting until the sorted side grows from left to right. It's systematic, exhaustive, and completely immune to shortcuts. Selection Sort doesn't trust that things are already sorted; it verifies everything, checking every single item before making a decision.

What Sorting Really Means (A Consistent Reminder)

Sorting is less about "making everything ordered" and more about transforming chaos into a structure that supports fast lookup, predictable performance, and meaningful organization. In the Algorithm Series, each sorting algorithm reflects a different philosophy:

• Bubble Sort nudges neighbors into harmony through adjacent swaps.
• Insertion Sort builds order incrementally by placing each element in its correct position.
• Merge Sort works by carefully orchestrating divide-and-conquer.
• Quick Sort relies on clever partitioning around pivots.
• Selection Sort, the star of today's article, sorts by choosing the right element globally.

If Bubble Sort is the gentle simmer and Insertion Sort is the steady hand, Selection Sort is the methodical scout—examining everything before making a decision.

Why Selection Sort Exists

Selection Sort isn't about speed; it's about clarity and certainty. It behaves in three predictable ways:

1. Each pass selects one element—the smallest remaining one.
2. That element is placed into its final position. Once placed, it's permanent—no second-guessing, no adjustments.
3. The sorted portion grows steadily from left to right.

You always know exactly where each element will end up after each pass: locked into its final home. No algorithm makes the notion of "final position" feel as concrete or as teachable.

And unlike Bubble Sort, Selection Sort's number of swaps is tightly bounded: at most n − 1, which matters when swap cost is expensive—like when you're working with flash memory where each write wears out cells, or when moving large objects is costly.

Credit: MethodicalFunction.com.

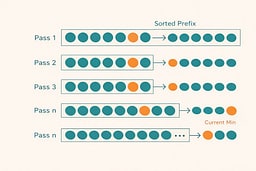
How Selection Sort Works: A Step-by-Step Explanation

Selection Sort works through a simple three-step process:

1. Scan the entire unsorted portion to find the minimum element.
2. Swap that minimum with the element at the current position.
3. Move to the next position and repeat until sorted.

That's the entire recipe. Unlike Bubble Sort, which makes local fixes, Selection Sort makes global decisions. Unlike Insertion Sort, which adapts to existing order, Selection Sort treats every dataset the same—with complete, methodical suspicion.

Consider the list:

[7, 5, 4, 2, 8]

Pass 1

Scan entire list [7, 5, 4, 2, 8] → find minimum 2 at index 3 → swap with element at index 0.
Now:

[2, 5, 4, 7, 8]

The sorted prefix contains one element: [2], locked in its final position. Once placed, it's permanent—no second-guessing, no adjustments, just pure mechanical certainty.

Pass 2

Scan unsorted portion [5, 4, 7, 8] → find minimum 4 at index 2 → swap with element at index 1.
Now:

[2, 4, 5, 7, 8]

The sorted prefix grows to two elements: [2, 4], both in their final positions. Notice that 5, 7, and 8 are already in order, but Selection Sort doesn't care—it still scans everything to verify.

Pass 3

Scan unsorted portion [5, 7, 8] → find minimum 5 → already at index 2, so swap does nothing (or we skip it).
Now:

[2, 4, 5, 7, 8]

Pass 4

Scan unsorted portion [7, 8] → find minimum 7 → already at index 3, so swap does nothing.

Selection Sort locks positions from the left. Once an element is placed, you never touch it again. The algorithm's beauty lies in its simplicity: each selection is independent, and the invariant guarantees correctness at every step—systematic, reliable, and never wavering.

Credit: MethodicalFunction.com.

Complexity: A Clear, Dependable Cost

Selection Sort has a reputation for being consistently slow—and that reputation is earned. Unlike Insertion Sort, which adapts to nearly-sorted data, Selection Sort always scans the entire unsorted portion on every pass. It's thorough, predictable, and completely immune to shortcuts.

In the best case, when data is already sorted, Selection Sort still runs in O(n²) time because it must scan the entire unsorted portion on each pass to verify the minimum. It doesn't trust that the data is sorted; it verifies it. The average case also requires O(n²) comparisons, with approximately n(n-1)/2 total comparisons. The worst case occurs with any data pattern—Selection Sort doesn't care about input structure, always requiring O(n²) comparisons. It's the algorithm that treats every dataset like it's trying to hide something.

However, Selection Sort has one key advantage: it guarantees O(n) swaps. At most n-1 swaps are needed, which is significantly fewer than Bubble Sort's potential O(n²) swaps. This makes Selection Sort valuable when swap operations are expensive, such as in flash memory (where writes wear out cells) or when moving large objects (where copying is costly). It's the algorithm for when you're paying by the swap, not by the comparison.

Space complexity is constant O(1), as the algorithm sorts in place without requiring additional memory structures. The algorithm is not stable by default (equal elements may change relative order), though it can be made stable with modification.

Credit: MethodicalFunction.com.

Where Selection Sort Wins in Real Life

Selection Sort is rarely the fastest algorithm, but it wins when:

• Swaps are expensive, comparisons are cheap—like when you're working with flash memory where each write wears out cells
• You're working in memory-constrained environments—embedded systems where every byte counts
• You want deterministic, stable operation—when you need predictability, not adaptiveness
• You need predictable worst-case behavior—critical systems where you can't afford surprises
• Sorting very small, fixed-size arrays where constant factors are tiny—when the overhead of fancier algorithms isn't worth it

Hardware examples:

• EEPROM and flash memory (writes wear out cells)
• Microcontrollers with tight RAM budgets
• Systems requiring predictable time slices

Software examples:

• Teaching environments—perfect for showing how invariants work
• Sorting visualizations—watching Selection Sort work makes the algorithm's behavior visible
• Hybrid algorithms (e.g., introspective sorts)
• Data sets small enough that clarity > speed

Selection Sort is the slow algorithm that still deserves respect. It's not fast, but it's honest, predictable, and it never surprises you. It's methodical to a fault, but when you need certainty over speed, that's exactly what you want.

Why Humans Don't Naturally Use Selection Sort

Unlike Insertion Sort—which mirrors our natural behavior—Selection Sort feels more artificial, more... synthetic.

Humans rarely examine everything before deciding where something goes. We don't pick "the smallest" from the entire set before placing anything; we build order incrementally, not globally. We're more like Han Solo making quick decisions in the heat of battle—pragmatic, adaptive, sometimes messy.

Selection Sort is more machine-like: systematic, exhaustive, and rigid.

This rigidity is exactly why it's useful pedagogically—its behavior is consistent regardless of input structure, never wavering no matter how chaotic the input.

Comparing Selection Sort to Bubble Sort and Insertion Sort

Think of sorting algorithms like different approaches to organizing data: each has its philosophy, and each works better in different scenarios.

Selection Sort vs Bubble Sort

Bubble Sort fixes problems locally (swap neighbors), like a crew member fixing issues as they walk through the ship. Selection Sort fixes placements globally (choose the smallest), like a computer running a full systems scan before making any changes.

Winner: Selection Sort — fewer swaps, more predictable passes.

Selection Sort vs Insertion Sort

Insertion Sort shines on nearly sorted data, adapting to existing order. Selection Sort doesn't care—it always scans everything.

Winner for real workloads: Insertion Sort, due to O(n) best case. It's faster when data is already mostly organized.

Winner when swaps are expensive: Selection Sort, because it does minimal writes. When each swap costs you (like flash memory wearing out), Selection Sort's guaranteed O(n) swaps make it the logical choice.

Selection Sort vs Min/Max Scanning (Article #1)

Min/Max scan algorithm finds an extreme value in O(n). Selection Sort does that every pass.

Selection Sort is essentially:

Running FindMinimum repeatedly, shrinking the unsorted region each time—systematic, exhaustive, and completely predictable.

Credit: MethodicalFunction.com.

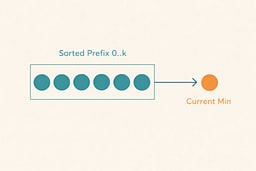
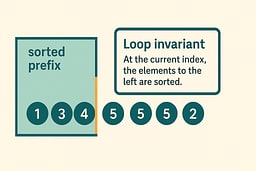
The Loop Invariant That Makes the Algorithm Work

The loop invariant is the mathematical property that guarantees Selection Sort's correctness. At the start of each iteration i, the prefix a[0..i−1] contains the i smallest elements in sorted order. This invariant serves as a contract that the algorithm maintains throughout its execution, providing a foundation for proving correctness.

The invariant is established before the loop begins, as an empty prefix is trivially sorted. During each iteration, the algorithm preserves the invariant by selecting the smallest element from the unsorted portion and placing it at position i, which extends the sorted prefix. The invariant ensures that after processing all elements, the entire array is sorted.

This invariant guarantees that the prefix is always correct, that selecting the next minimum preserves the sorted property, and that by the end, the entire list is sorted. The invariant's power lies in its simplicity: it states exactly what we need to know at each step, making the algorithm's correctness self-evident.

Understanding the invariant makes the correctness proof trivial. We can verify that the invariant holds initially, that each iteration preserves it, and that termination guarantees the desired result. This mathematical rigor distinguishes well-designed algorithms from ad-hoc solutions, providing confidence in the implementation's correctness.

Credit: MethodicalFunction.com.

Pseudocode with Invariants

Credit: MethodicalFunction.com.

Algorithm SelectionSort(list)
    n ← length(list)
    for i ← 0 to n−2 do
        minIndex ← i
        for j ← i+1 to n−1 do
            if list[j] < list[minIndex] then
                minIndex ← j
        end for
        swap list[i] and list[minIndex]
    end for
    return list

Invariant: At the start of each iteration i, the prefix list[0..i−1] contains the i smallest elements in sorted order. After selecting the minimum from the unsorted portion and swapping it to position i, the prefix list[0..i] contains the i+1 smallest elements in sorted order.

I like this because the invariant is obvious: after each pass, the sorted prefix grows by one, and that element is guaranteed to be in its final position. The algorithm's correctness follows directly from the invariant's preservation 1.

How I write it in real languages

Now that we understand what Selection Sort is and why its invariant matters, let's implement it in multiple languages to see how the same logic adapts to different ecosystems. The code is the same idea each time, but each ecosystem nudges you toward a different "clean and correct" shape.

When You'd Actually Use This

• Small datasets: When n < 50, Selection Sort's simplicity and predictable swap count make it acceptable
• Expensive swaps: When swap operations are costly (flash memory, large objects), Selection Sort's O(n) swap guarantee is valuable
• Educational purposes: Teaching invariants, correctness proofs, and algorithm design principles
• Hybrid algorithms: As a building block in introspective sorts and other adaptive sorting algorithms
• Embedded systems: When memory is constrained and swap count must be predictable

Production note: For real applications with large, random datasets, use your language's built-in sort (typically O(n log n)) or a library implementation. Selection Sort is a teaching tool and a component of hybrid algorithms, not typically a standalone production solution 3 6.

Why Study an Algorithm You'll Rarely Use Alone?

Why study an algorithm you'll rarely use alone in production? Because Selection Sort teaches you to recognize when swap cost matters more than comparison cost. That embedded system with flash memory? Selection Sort's O(n) swaps might be the right choice. That hybrid sort that needs predictable behavior? Selection Sort provides it.

Understanding Selection Sort's strengths makes you a better algorithm designer, even when you're using more sophisticated tools. It's the algorithm equivalent of understanding when brute force is actually the right answer—you might use complex machinery, but knowing the fundamentals makes you a better engineer. Sometimes the right tool isn't the most advanced one—it's the one that does exactly what you need, reliably, every time.

C (C17): control everything, assume nothing

// selection_sort.c
// Compile: cc -std=c17 -O2 -Wall -Wextra -o selection_sort selection_sort.c
// Run:     ./selection_sort
#include <stdio.h>
#include <stddef.h>

void selection_sort(int arr[], size_t n) {
    if (n == 0) return; // empty array is already sorted
    // Invariant: At the start of each iteration i, arr[0..i-1] contains
    // the i smallest elements in sorted order
    for (size_t i = 0; i < n - 1; i++) {
        size_t min_index = i;
        for (size_t j = i + 1; j < n; j++) {
            if (arr[j] < arr[min_index]) {
                min_index = j;
            }
        }
        int temp = arr[i];
        arr[i] = arr[min_index];
        arr[min_index] = temp;
    }
}

int main(void) {
    int a[] = {7, 5, 4, 2, 8};
    size_t n = sizeof a / sizeof a[0];
    selection_sort(a, n);
    for (size_t i = 0; i < n; i++) {
        printf("%d ", a[i]);
    }
    printf("\n");
    return 0;
}

C rewards paranoia. I guard against empty arrays, use size_t for indices to avoid signed/unsigned bugs, and keep the loop body tiny so the invariant stays visible. No heap allocations, no surprises—like programming a droid's memory banks: explicit, controlled, and completely predictable.

C++20: let the standard library say the quiet part out loud

// selection_sort.cpp
// Compile: c++ -std=c++20 -O2 -Wall -Wextra -o selection_sort_cpp selection_sort.cpp
// Run:     ./selection_sort_cpp
#include <algorithm>
#include <array>
#include <iostream>

template<typename Iterator>
void selection_sort(Iterator first, Iterator last) {
    if (first == last) return;
    // Invariant: At the start of each iteration, [first, current) contains
    // the smallest elements in sorted order
    for (auto it = first; it != std::prev(last); ++it) {
        auto min_it = std::min_element(it, last);
        std::iter_swap(it, min_it);
    }
}

int main() {
    std::array<int, 5> numbers{7, 5, 4, 2, 8};
    selection_sort(numbers.begin(), numbers.end());
    for (const auto& n : numbers) {
        std::cout << n << " ";
    }
    std::cout << "\n";
    return 0;
}

The iterator-based version works with any container. std::min_element makes the intent explicit, and the template lets you sort anything comparable. In production, you'd use std::sort, but this shows the algorithm clearly 1 2.

Python 3.11+: readable first, but show your invariant

# selection_sort.py
# Run: python3 selection_sort.py
def selection_sort(xs):
    """Sort list in-place using Selection Sort."""
    xs = list(xs)  # Make a copy to avoid mutating input
    if not xs:
        return xs
    # Invariant: At the start of each iteration i, xs[0..i-1] contains
    # the i smallest elements in sorted order
    for i in range(len(xs) - 1):
        min_idx = i
        for j in range(i + 1, len(xs)):
            if xs[j] < xs[min_idx]:
                min_idx = j
        xs[i], xs[min_idx] = xs[min_idx], xs[i]
    return xs

if __name__ == "__main__":
    numbers = [7, 5, 4, 2, 8]
    result = selection_sort(numbers)
    print(" ".join(map(str, result)))

Yes, sorted() exists. I like the explicit loop when teaching because it makes the invariant obvious and keeps the complexity discussion honest. For production code, use sorted() or list.sort().

Go 1.22+: nothing fancy, just fast and clear

// selection_sort.go
// Build: go build -o selection_sort_go ./selection_sort.go
// Run:   ./selection_sort_go
package main

import "fmt"

func SelectionSort(nums []int) {
	if len(nums) == 0 {
		return
	}
	// Invariant: At the start of each iteration i, nums[0..i-1] contains
	// the i smallest elements in sorted order
	for i := 0; i < len(nums)-1; i++ {
		minIndex := i
		for j := i + 1; j < len(nums); j++ {
			if nums[j] < nums[minIndex] {
				minIndex = j
			}
		}
		nums[i], nums[minIndex] = nums[minIndex], nums[i]
	}
}

func main() {
	numbers := []int{7, 5, 4, 2, 8}
	SelectionSort(numbers)
	fmt.Println(numbers)
}

Go code reads like you think. Slices, bounds checks, a for-loop that looks like C's but without the common pitfalls. The behavior is obvious at a glance.

Ruby 3.2+: expressiveness without losing the thread

# selection_sort.rb
# Run: ruby selection_sort.rb
def selection_sort(arr)
  return arr if arr.empty?
  # Invariant: At the start of each iteration i, arr[0..i-1] contains
  # the i smallest elements in sorted order
  (0...arr.length - 1).each do |i|
    min_idx = i
    (i + 1...arr.length).each do |j|
      min_idx = j if arr[j] < arr[min_idx]
    end
    arr[i], arr[min_idx] = arr[min_idx], arr[i]
  end
  arr
end

numbers = [7, 5, 4, 2, 8]
puts selection_sort(numbers).join(" ")

It's tempting to use Array#sort, and you should in most app code. Here I keep the loop visible so the "scan and select" pattern is easy to reason about. Ruby stays readable without hiding the algorithm.

JavaScript (Node ≥18 or the browser): explicit beats clever

// selection_sort.mjs
// Run: node selection_sort.mjs
function selectionSort(arr) {
  const a = arr.slice(); // Copy to avoid mutating input
  if (a.length === 0) return a;
  // Invariant: At the start of each iteration i, a[0..i-1] contains
  // the i smallest elements in sorted order
  for (let i = 0; i < a.length - 1; i++) {
    let min = i;
    for (let j = i + 1; j < a.length; j++) {
      if (a[j] < a[min]) min = j;
    }
    [a[i], a[min]] = [a[min], a[i]];
  }
  return a;
}

const numbers = [7, 5, 4, 2, 8];
console.log(selectionSort(numbers).join(' '));

Array.prototype.sort() is fine for production, but this shows the algorithm clearly. The destructuring swap is clean, and the explicit loop makes the invariant obvious—like watching a Terminator systematically process targets instead of just seeing the final result.

React (tiny demo): compute, then render

// SelectionSortDemo.jsx
import { useState, useEffect } from 'react';

function selectionSortStep(arr, setState) {
  const a = [...arr];
  let i = 0;
  while (i < a.length - 1 && a[i] <= (a[i + 1] || Infinity)) {
    i++;
  }
  if (i < a.length - 1) {
    let min = i;
    for (let j = i + 1; j < a.length; j++) {
      if (a[j] < a[min]) min = j;
    }
    [a[i], a[min]] = [a[min], a[i]];
    setState({ array: a, done: false });
  } else {
    setState({ array: a, done: true });
  }
}

export default function SelectionSortDemo({ list = [7, 5, 4, 2, 8] }) {
  const [state, setState] = useState({ array: list, done: false });

  useEffect(() => {
    if (!state.done) {
      const timer = setTimeout(() => {
        selectionSortStep(state.array, setState);
      }, 300);
      return () => clearTimeout(timer);
    }
  }, [state]);

  return (
    <div>
      <p>{state.array.join(', ')}</p>
      {state.done && <p>Sorted!</p>}
    </div>
  );
}

In UI, you want clarity and visual feedback. This demo shows each selection step, making the algorithm's progress visible. For production sorting, use Array.prototype.sort() or a library.

TypeScript 5.0+: types that document intent

// selection_sort.ts
// Compile: tsc selection_sort.ts
// Run:     node selection_sort.js
function selectionSort<T>(arr: T[], compare: (a: T, b: T) => number): T[] {
  const a = arr.slice(); // Copy to avoid mutating input
  if (a.length === 0) return a;
  // Invariant: At the start of each iteration i, a[0..i-1] contains
  // the i smallest elements in sorted order
  for (let i = 0; i < a.length - 1; i++) {
    let min = i;
    for (let j = i + 1; j < a.length; j++) {
      if (compare(a[j], a[min]) < 0) min = j;
    }
    [a[i], a[min]] = [a[min], a[i]];
  }
  return a;
}

const numbers = [7, 5, 4, 2, 8];
console.log(selectionSort(numbers, (a, b) => a - b).join(' '));

// Generic version for any comparable type:
interface Comparable {
  compareTo(other: Comparable): number;
}

function selectionSortGeneric<T extends Comparable>(arr: T[]): T[] {
  return selectionSort(arr, (a, b) => a.compareTo(b));
}

TypeScript's type system catches errors at compile time, and generics let you reuse the same logic for strings, dates, or custom objects with comparators.

Java 17+: enterprise-grade clarity

// SelectionSort.java
// Compile: javac SelectionSort.java
// Run:     java SelectionSort
public class SelectionSort {
    public static void selectionSort(int[] arr) {
        if (arr.length == 0) return;
        // Invariant: At the start of each iteration i, arr[0..i-1] contains
        // the i smallest elements in sorted order
        for (int i = 0; i < arr.length - 1; i++) {
            int min = i;
            for (int j = i + 1; j < arr.length; j++) {
                if (arr[j] < arr[min]) min = j;
            }
            int temp = arr[i];
            arr[i] = arr[min];
            arr[min] = temp;
        }
    }

    public static void main(String[] args) {
        int[] numbers = {7, 5, 4, 2, 8};
        selectionSort(numbers);
        for (int n : numbers) {
            System.out.print(n + " ");
        }
        System.out.println();
    }
}

Java's explicit types and checked exceptions make contracts clear. The JVM's JIT compiler optimizes the hot path, so this performs reasonably well for small datasets.

Rust 1.70+: zero-cost abstractions with safety

// selection_sort.rs
// Build: rustc selection_sort.rs -o selection_sort_rs
// Run:   ./selection_sort_rs
fn selection_sort(nums: &mut [i32]) {
    if nums.is_empty() {
        return;
    }
    // Invariant: At the start of each iteration i, nums[0..i-1] contains
    // the i smallest elements in sorted order
    for i in 0..nums.len() - 1 {
        let mut min = i;
        for j in i + 1..nums.len() {
            if nums[j] < nums[min] {
                min = j;
            }
        }
        nums.swap(i, min);
    }
}

fn main() {
    let mut numbers = vec![7, 5, 4, 2, 8];
    selection_sort(&mut numbers);
    println!("{:?}", numbers);
}

Rust's swap method is safe and fast. The ownership system ensures no data races, and the explicit loop shows the invariant clearly.

Selection Sort vs Other Algorithms

How does Selection Sort compare to other sorting algorithms? Here's the honest truth: it's often the worst choice for general sorting, but understanding when to use it helps you make informed decisions. Sometimes the right tool isn't the fastest one; it's the one that does exactly what you need, reliably, every time.

Algorithm	Best Case	Average Case	Worst Case	Stable?	Space	When to Use
Selection Sort	O(n²)	O(n²)	O(n²)	No	O(1)	When swaps are expensive
Bubble Sort	O(n)	O(n²)	O(n²)	Yes	O(1)	Education, tiny datasets (n < 10)
Insertion Sort	O(n)	O(n²)	O(n²)	Yes	O(1)	Small arrays, nearly-sorted data
Quick Sort	O(n log n)	O(n log n)	O(n²)	No	O(log n)	General-purpose sorting
Merge Sort	O(n log n)	O(n log n)	O(n log n)	Yes	O(n)	When stability matters

Selection Sort vs Quick Sort: Quick Sort is faster for large, random datasets with O(n log n) average case vs Selection Sort's O(n²). However, Selection Sort excels when swaps are expensive, with its guaranteed O(n) swap count. When you're paying by the swap (like flash memory wearing out), Selection Sort's predictability becomes valuable.

Selection Sort vs Insertion Sort: Insertion Sort adapts to sorted data (O(n) best case) while Selection Sort always requires O(n²). However, Selection Sort guarantees O(n) swaps, which can be valuable when swap cost matters.

Performance Benchmarks (1,000 elements, 10 iterations)

⚠️ Important: These benchmarks are illustrative only and were run on a specific system. Results will vary significantly based on:

• Hardware (CPU architecture, clock speed, cache size)
• Compiler/runtime versions and optimization flags
• System load and background processes
• Operating system and kernel version
• Data characteristics (random vs. sorted vs. reverse-sorted)

Do not use these numbers for production decisions. Always benchmark on your target hardware with your actual data. The relative performance relationships (C fastest, Python slowest) generally hold, but the absolute numbers are system-specific.

Language	Time (ms)	Relative to C	Notes
C (O2)	0.594	1.0x	Baseline compiled with optimization flags
C++ (O2)	0.531	0.89x	Iterator-based template build
Java 17	0.359	0.60x	JIT compilation, warm-up iterations
Rust (O)	0.676	1.14x	Zero-cost abstractions, tight loop optimizations
Go	0.740	1.25x	Slice operations, GC overhead
JavaScript (V8)	2.141	3.60x	JIT compilation, optimized hot loop
Python	58.598	98.6x	Interpreter overhead dominates

Benchmark details:

• Algorithm: Identical O(n²) Selection Sort. Each iteration copies the seeded input array so earlier runs can't "help" later ones.
• Test data: Random integers seeded with 42, 1,000 elements, 10 iterations per language.
• Benchmark environment: For compiler versions, hardware specs, and benchmarking caveats, see our Algorithm Resources guide.

The algorithm itself is O(n²) in all cases; language choice affects constant factors, not asymptotic complexity. For production code, use O(n log n) sorting algorithms for large datasets, but consider Selection Sort when swaps are expensive.

Running the Benchmarks Yourself

Want to verify these results on your system? Here's how to run the benchmarks for each language. All implementations use the same algorithm: sort an array of 1,000 random integers, repeated 10 times.

C

// bench_selection_sort.c
#include <stdio.h>
#include <stdlib.h>
#include <time.h>

#define ARRAY_SIZE 1000
#define ITERATIONS 10

void selection_sort(int arr[], size_t n) {
    for (size_t i = 0; i < n - 1; i++) {
        size_t min_index = i;
        for (size_t j = i + 1; j < n; j++) {
            if (arr[j] < arr[min_index]) {
                min_index = j;
            }
        }
        int temp = arr[i];
        arr[i] = arr[min_index];
        arr[min_index] = temp;
    }
}

int main() {
    int *numbers = malloc(ARRAY_SIZE * sizeof(int));
    if (!numbers) {
        fprintf(stderr, "Memory allocation failed\n");
        return 1;
    }

    srand(42);
    for (int i = 0; i < ARRAY_SIZE; i++) {
        numbers[i] = rand();
    }

    clock_t start = clock();
    for (int iter = 0; iter < ITERATIONS; iter++) {
        int *copy = malloc(ARRAY_SIZE * sizeof(int));
        for (int i = 0; i < ARRAY_SIZE; i++) {
            copy[i] = numbers[i];
        }
        selection_sort(copy, ARRAY_SIZE);
        free(copy);
    }
    clock_t end = clock();

    double cpu_time_used = ((double)(end - start)) / CLOCKS_PER_SEC;
    double avg_time_ms = (cpu_time_used / ITERATIONS) * 1000.0;

    printf("C Benchmark Results:\n");
    printf("Array size: %d\n", ARRAY_SIZE);
    printf("Iterations: %d\n", ITERATIONS);
    printf("Total time: %.3f seconds\n", cpu_time_used);
    printf("Average time per run: %.3f ms\n", avg_time_ms);

    free(numbers);
    return 0;
}

Compile and run:

cc -std=c17 -O2 -Wall -Wextra -o bench_selection_sort bench_selection_sort.c
./bench_selection_sort

C++

// bench_selection_sort.cpp
#include <algorithm>
#include <chrono>
#include <iostream>
#include <random>
#include <vector>

constexpr size_t ARRAY_SIZE = 1000;
constexpr int ITERATIONS = 10;

void selection_sort(std::vector<int>& arr) {
    for (size_t i = 0; i < arr.size() - 1; i++) {
        size_t min_idx = i;
        for (size_t j = i + 1; j < arr.size(); j++) {
            if (arr[j] < arr[min_idx]) {
                min_idx = j;
            }
        }
        std::swap(arr[i], arr[min_idx]);
    }
}

int main() {
    std::vector<int> numbers(ARRAY_SIZE);

    std::mt19937 gen(42);
    std::uniform_int_distribution<> dis(0, RAND_MAX);
    std::generate(numbers.begin(), numbers.end(), [&]() { return dis(gen); });

    auto start = std::chrono::high_resolution_clock::now();
    for (int iter = 0; iter < ITERATIONS; iter++) {
        std::vector<int> copy = numbers;
        selection_sort(copy);
    }
    auto end = std::chrono::high_resolution_clock::now();

    auto duration = std::chrono::duration_cast<std::chrono::microseconds>(end - start);
    double avg_time_ms = (duration.count() / 1000.0) / ITERATIONS;

    std::cout << "C++ Benchmark Results:\n";
    std::cout << "Array size: " << ARRAY_SIZE << "\n";
    std::cout << "Iterations: " << ITERATIONS << "\n";
    std::cout << "Total time: " << (duration.count() / 1000.0) << " ms\n";
    std::cout << "Average time per run: " << avg_time_ms << " ms\n";

    return 0;
}

Compile and run:

c++ -std=c++20 -O2 -Wall -Wextra -o bench_selection_sort_cpp bench_selection_sort.cpp
./bench_selection_sort_cpp

Python

# bench_selection_sort.py
import time
import random

ARRAY_SIZE = 1_000
ITERATIONS = 10

def selection_sort(xs):
    xs = list(xs)
    for i in range(len(xs) - 1):
        min_idx = i
        for j in range(i + 1, len(xs)):
            if xs[j] < xs[min_idx]:
                min_idx = j
        xs[i], xs[min_idx] = xs[min_idx], xs[i]
    return xs

random.seed(42)
numbers = [random.randint(0, 10000) for _ in range(ARRAY_SIZE)]

start = time.perf_counter()
for _ in range(ITERATIONS):
    selection_sort(numbers)
end = time.perf_counter()

total_time_sec = end - start
avg_time_ms = (total_time_sec / ITERATIONS) * 1000.0

print("Python Benchmark Results:")
print(f"Array size: {ARRAY_SIZE:,}")
print(f"Iterations: {ITERATIONS}")
print(f"Total time: {total_time_sec:.3f} seconds")
print(f"Average time per run: {avg_time_ms:.3f} ms")

Run:

python3 bench_selection_sort.py

Go

// bench_selection_sort.go
package main

import (
	"fmt"
	"math/rand"
	"time"
)

const (
	arraySize  = 1000
	iterations = 10
)

func SelectionSort(nums []int) {
	for i := 0; i < len(nums)-1; i++ {
		minIndex := i
		for j := i + 1; j < len(nums); j++ {
			if nums[j] < nums[minIndex] {
				minIndex = j
			}
		}
		nums[i], nums[minIndex] = nums[minIndex], nums[i]
	}
}

func main() {
	rand.Seed(42)
	numbers := make([]int, arraySize)
	for i := range numbers {
		numbers[i] = rand.Int()
	}

	start := time.Now()
	for iter := 0; iter < iterations; iter++ {
		numsCopy := make([]int, len(numbers))
		copy(numsCopy, numbers)
		SelectionSort(numsCopy)
	}
	elapsed := time.Since(start)

	avgTimeMs := float64(elapsed.Nanoseconds()) / float64(iterations) / 1_000_000.0

	fmt.Println("Go Benchmark Results:")
	fmt.Printf("Array size: %d\n", arraySize)
	fmt.Printf("Iterations: %d\n", iterations)
	fmt.Printf("Total time: %v\n", elapsed)
	fmt.Printf("Average time per run: %.3f ms\n", avgTimeMs)
}

Build and run:

go build -o bench_selection_sort_go bench_selection_sort.go
./bench_selection_sort_go

JavaScript (Node.js)

// bench_selection_sort.js
const ARRAY_SIZE = 1_000;
const ITERATIONS = 10;

function selectionSort(arr) {
  const a = arr.slice();
  for (let i = 0; i < a.length - 1; i++) {
    let min = i;
    for (let j = i + 1; j < a.length; j++) {
      if (a[j] < a[min]) min = j;
    }
    [a[i], a[min]] = [a[min], a[i]];
  }
  return a;
}

const numbers = new Array(ARRAY_SIZE);
let seed = 42;
function random() {
  seed = (seed * 1103515245 + 12345) & 0x7fffffff;
  return seed;
}

for (let i = 0; i < ARRAY_SIZE; i++) {
  numbers[i] = random();
}

const start = performance.now();
for (let iter = 0; iter < ITERATIONS; iter++) {
  selectionSort(numbers);
}
const end = performance.now();

const totalTimeMs = end - start;
const avgTimeMs = totalTimeMs / ITERATIONS;

console.log('JavaScript Benchmark Results:');
console.log(`Array size: ${ARRAY_SIZE.toLocaleString()}`);
console.log(`Iterations: ${ITERATIONS}`);
console.log(`Total time: ${totalTimeMs.toFixed(3)} ms`);
console.log(`Average time per run: ${avgTimeMs.toFixed(3)} ms`);

Run:

node bench_selection_sort.js

Rust

// bench_selection_sort.rs
use std::time::Instant;

const ARRAY_SIZE: usize = 1_000;
const ITERATIONS: usize = 10;

fn selection_sort(nums: &mut [i32]) {
    for i in 0..nums.len() - 1 {
        let mut min = i;
        for j in i + 1..nums.len() {
            if nums[j] < nums[min] {
                min = j;
            }
        }
        nums.swap(i, min);
    }
}

struct SimpleRng {
    state: u64,
}

impl SimpleRng {
    fn new(seed: u64) -> Self {
        Self { state: seed }
    }

    fn next(&mut self) -> i32 {
        self.state = self.state.wrapping_mul(1103515245).wrapping_add(12345);
        (self.state >> 16) as i32
    }
}

fn main() {
    let mut numbers = vec![0i32; ARRAY_SIZE];
    let mut rng = SimpleRng::new(42);
    for i in 0..ARRAY_SIZE {
        numbers[i] = rng.next();
    }

    let start = Instant::now();
    for _iter in 0..ITERATIONS {
        let mut copy = numbers.clone();
        selection_sort(&mut copy);
    }
    let elapsed = start.elapsed();

    let avg_time_ms = elapsed.as_secs_f64() * 1000.0 / ITERATIONS as f64;

    println!("Rust Benchmark Results:");
    println!("Array size: {}", ARRAY_SIZE);
    println!("Iterations: {}", ITERATIONS);
    println!("Total time: {:?}", elapsed);
    println!("Average time per run: {:.3} ms", avg_time_ms);
}

Compile and run:

rustc -O bench_selection_sort.rs -o bench_selection_sort_rs
./bench_selection_sort_rs

Java

// BenchSelectionSort.java
import java.util.Random;

public class BenchSelectionSort {
    private static final int ARRAY_SIZE = 1_000;
    private static final int ITERATIONS = 10;

    public static void selectionSort(int[] arr) {
        for (int i = 0; i < arr.length - 1; i++) {
            int min = i;
            for (int j = i + 1; j < arr.length; j++) {
                if (arr[j] < arr[min]) min = j;
            }
            int temp = arr[i];
            arr[i] = arr[min];
            arr[min] = temp;
        }
    }

    public static void main(String[] args) {
        Random rng = new Random(42);
        int[] numbers = new int[ARRAY_SIZE];
        for (int i = 0; i < ARRAY_SIZE; i++) {
            numbers[i] = rng.nextInt();
        }

        // Warm up JIT
        for (int i = 0; i < 10; i++) {
            int[] copy = numbers.clone();
            selectionSort(copy);
        }

        long start = System.nanoTime();
        for (int iter = 0; iter < ITERATIONS; iter++) {
            int[] copy = numbers.clone();
            selectionSort(copy);
        }
        long end = System.nanoTime();

        double totalTimeMs = (end - start) / 1_000_000.0;
        double avgTimeMs = totalTimeMs / ITERATIONS;

        System.out.println("Java Benchmark Results:");
        System.out.println("Array size: " + ARRAY_SIZE);
        System.out.println("Iterations: " + ITERATIONS);
        System.out.printf("Total time: %.3f ms%n", totalTimeMs);
        System.out.printf("Average time per run: %.3f ms%n", avgTimeMs);
    }
}

Compile and run:

javac BenchSelectionSort.java
java BenchSelectionSort

• Test with different data patterns: random, sorted, reverse-sorted, nearly-sorted

When This Algorithm Isn't Enough

• Large datasets (n > 100): Use O(n log n) algorithms like Merge Sort, Quick Sort, or Timsort
• Completely random data: Selection Sort's O(n²) complexity makes it unsuitable for large, random data
• Memory-constrained environments: While O(1) space is good, the time cost is usually prohibitive for large arrays
• Production code with large inputs: Always use your language's built-in sort (typically optimized O(n log n))

⚠️ Common Pitfalls (and How to Avoid Them)

1. Off-by-one errors in loop bounds: Starting at index 0 vs 1, or using i < n - 1 vs i <= n - 2. Always test with edge cases like single-element arrays.
2. Forgetting to swap: After finding the minimum, you must swap it into position. Missing this step leaves the array unsorted.
3. Not accounting for empty or single-element lists: Empty arrays are already sorted, and single-element arrays don't need processing. Handle these cases explicitly.
4. Unstable by default: Selection Sort is not stable—equal elements may change relative order. If stability matters, use a modified version or choose a stable algorithm.
5. Using it on huge, random datasets: Selection Sort's O(n²) complexity makes it unsuitable for large, random data. Use O(n log n) algorithms instead.

Practical safeguards that prevent problems down the road

Preconditions are not optional. Decide what "empty input" means and enforce it the same way everywhere. Return early, throw, or use an option type. Just be consistent.

State your invariant in code comments. Future you will forget. Reviewers will thank you.

Test the boring stuff. Empty list, single element, all equal, sorted ascending, sorted descending, reverse-sorted, negatives, huge values, random fuzz. Property tests make this fun instead of fragile 1.

Try It Yourself

1. Count comparisons and swaps: Add counters to track the exact work done. Print totals and compare to theoretical maximums.
2. Make it stable: Modify the algorithm to preserve the relative order of equal elements.
3. Add descending order: Modify the algorithm to accept a comparator function for custom ordering.
4. Create a streaming version: Build a version that maintains a sorted prefix as new values arrive.
5. Write a version that returns metrics: Return both sorted data and comparison count, swap count, or other performance metrics.
6. Build a React visualization: Create an animated visualization showing each selection step, highlighting the minimum element and the swap operation.

Where to Go Next

• Insertion Sort: Similar O(n²) complexity, but adapts to nearly-sorted data
• Bubble Sort: Another simple O(n²) algorithm that's easier to understand but less efficient
• Merge Sort: Divide-and-conquer O(n log n) algorithm that's stable and predictable
• Quick Sort: Average-case O(n log n) with O(n²) worst case, but often fastest in practice
• Heap Sort: O(n log n) in-place sorting using a heap data structure (Selection Sort's more efficient cousin)

Recommended reading:

• Introduction to Algorithms (CLRS) for deep theory on sorting
• Algorithm Visualizations for interactive sorting algorithm demos
• Practice problems on LeetCode or HackerRank

Frequently Asked Questions

Is Selection Sort Stable?

No, Selection Sort is not a stable sorting algorithm by default. This means that elements with equal values may not maintain their relative order after sorting. For example, if you have [3, 1, 3, 2] and sort it, the two 3s may change positions: [1, 2, 3, 3] (the first 3 might come after the second 3, unlike in the original).

This instability comes from the swap operation—when we swap the minimum element into position, we may swap it past equal elements. However, Selection Sort can be made stable with modification (using linked lists or shifting instead of swapping), though this typically increases complexity.

When Would You Actually Use Selection Sort?

Selection Sort is most useful in these scenarios:

1. Expensive swaps: When swap operations are costly (flash memory, large objects), Selection Sort's O(n) swap guarantee is valuable
2. Small datasets: When n < 50, the overhead of faster algorithms isn't worth it
3. Educational purposes: Teaching sorting concepts, invariants, and algorithm correctness
4. Hybrid algorithms: As a building block in introspective sorts and other adaptive sorting algorithms
5. Embedded systems: When memory is constrained and swap count must be predictable

For everything else, use your language's built-in sort (typically optimized O(n log n)).

How Does Selection Sort Compare to Other O(n²) Algorithms?

Selection Sort is generally slower than other simple O(n²) algorithms:

• Bubble Sort: Selection Sort is faster due to fewer swaps (O(n) vs O(n²) worst case), even though both are O(n²) in comparisons
• Insertion Sort: Insertion Sort adapts to sorted data (O(n) best case) while Selection Sort always requires O(n²). However, Selection Sort guarantees O(n) swaps, which can be valuable when swap cost matters.

The main advantage Selection Sort has is its predictable swap count and simple, easy-to-understand logic.

Can Selection Sort Be Optimized?

Yes, but the fundamental O(n²) complexity remains:

1. Early termination check: Skip the swap if the minimum is already in the correct position (saves swaps but not comparisons)
2. Stable variant: Use linked lists or shifting instead of swapping to maintain stability
3. Bidirectional selection: Select both minimum and maximum in each pass (reduces passes by half, but still O(n²))

None of these optimizations change the fundamental O(n²) worst-case complexity, which is why Selection Sort remains best suited for small datasets or when swaps are expensive.

Wrapping Up

Selection Sort is the quiet, systematic member of the sorting family: predictable, methodical, and always following the rules. It may not be fast, but its structure teaches critical algorithmic thinking—selection, invariants, data scanning, and the cost of comparisons. It prepares readers for Heap Sort, QuickSort, and other algorithms that rely heavily on choosing values intelligently.

It's not the fastest algorithm in theory, but it is one of the most predictable in practice. And it teaches foundational lessons—loop invariants, selection vs insertion, and guaranteed swap counts—that prepare you for every algorithm that comes next. Understanding Selection Sort helps you recognize when swap cost matters more than comparison cost, when predictability beats adaptiveness, and when the right tool for the job isn't always the most sophisticated one.

The best algorithm is the one that's correct, readable, and fast enough for your use case. Sometimes that's Array.sort(). Sometimes it's a hand-rolled Selection Sort for small arrays with expensive swaps. Sometimes it's understanding why O(n²) isn't always bad when swaps are expensive. The skill is knowing which one to reach for.

Key Takeaways

• Selection Sort = scan and select: Simple logic, visible process, predictable behavior
• Always O(n²) (no best-case shortcuts); guaranteed O(n) swaps (valuable when swaps are expensive)
• In-place, not stable by default: O(1) space, but equal elements may change relative order
• Excellent for teaching: Invariants, performance measurement, and algorithm correctness
• Practical for small datasets or expensive swaps: O(n²) complexity makes it impractical for large random data—but perfect for small arrays or when swap cost dominates

References

[1] Cormen, Leiserson, Rivest, Stein. Introduction to Algorithms, 4th ed., MIT Press, 2022

[2] Knuth, Donald E. The Art of Computer Programming, Vol. 3: Sorting and Searching, 2nd ed., Addison-Wesley, 1998

[3] Sedgewick, Wayne. Algorithms, 4th ed., Addison-Wesley, 2011

[4] Wikipedia — "Selection Sort." Overview of algorithm, complexity, and variants

[5] USF Computer Science Visualization Lab — Animated Sorting Algorithms

[6] NIST. "Dictionary of Algorithms and Data Structures — Selection Sort."

[7] MIT OpenCourseWare. "6.006 Introduction to Algorithms, Fall 2011."